

To encrypt a message, each block of n letters (considered as an n-component vector) is multiplied by an invertible n × n matrix, against modulus 26. Often the simple scheme A = 0, B = 1, …, Z = 25 is used, but this is not an essential feature of the cipher. Each letter is represented by a number modulo 26. Hill cipher is a polygraphic substitution cipher based on linear algebra. The Hill cipher was invented by Lester S. Text_d = input( "What text would you like to decrypt?: ") Text_e = input( "What text would you like to encrypt?: ") Print( "Would you like to encrypt or decrypt some text? (1 or 2)") Hc = HillCipher(numpy.array(hill_matrix)) Print( "Enter each row of the encryption key with space separated integers") N = int( input( "Enter the order of the encryption key: ")) Self.replace_digits(num) for num in batch_decrypted
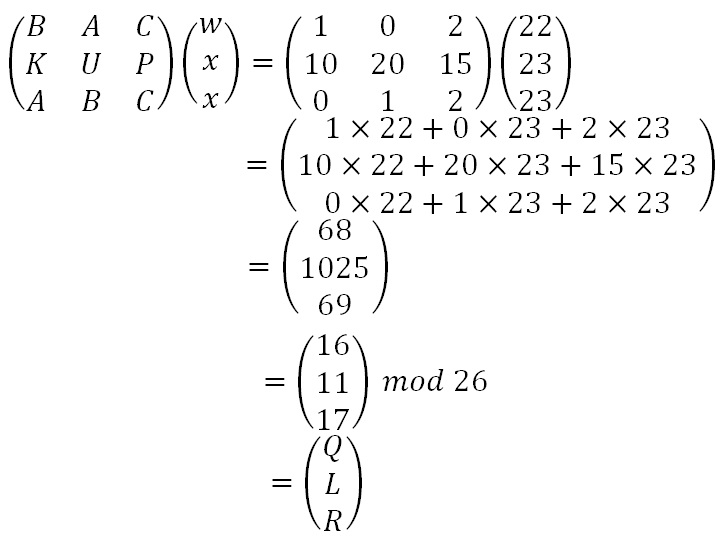
> hill_crypt('WHXYJOLM9C6XT085LL')ĭecrypted = "" for i in range( 0, len(text) - self.break_key + 1, self.break_key):īatch_decrypted = self.modulus(decrypt_key.dot(batch_vec)).T.tolist() Self.replace_digits(num) for num in batch_encryptedĭef make_decrypt_key( self) -> numpy.ndarray: Vec = īatch_encrypted = self.modulus(self.encrypt_key.dot(batch_vec)).T.tolist()[ > hill_cipher.encrypt('testing hill cipher')Įncrypted = "" for i in range( 0, len(text) - self.break_key + 1, self.break_key): > hill_cipher.process_text('Testing Hill Cipher')Ĭhars = > hill_cipher = HillCipher(numpy.array(, ]))ĭef replace_digits( self, num: int) -> str:ĭet = round((self.encrypt_key)) Self.check_determinant() # validate the determinant of the encryption keyĭef replace_letters( self, letter: str) -> int: Self.encrypt_key = self.modulus(encrypt_key) # mod36 calc's on the encrypt key Modulus = numpy.vectorize( lambda x: x % 36)ĭef _init_( self, encrypt_key: numpy.ndarray) -> None: a total of 36 characters # take x and return x % len(key_string) # This cipher takes alphanumerics into account # i.e. Key_string = string.ascii_uppercase + string.digits """ return b if a = 0 else greatest_common_divisor(b % a, a) So the text afterĭecrypting might be a little different than the original text.ĭef greatest_common_divisor( a: int, b: int) -> int: Length of the text reaches a multiple of the break_key. The text to be encrypted is not a multiple of the break key(the length of oneīatch of letters), the last character of the text is added to the text until the This implementation only considers alphanumerics in the text. The determinant of the encryption key matrix must be relatively prime w.r.t 36. The same process is repeated for decrypting to get While decrypting, the decrypting key is found which is the inverse of theĮncrypting key modular 36. On the vectors so as to bring the numbers between 0 and 36 and then mapped with After each multiplication modular 36 calculations are performed The key is then multiplied with the newly created batch vector to obtain theĮncoded vector. Your text is divided into batches of length N and converted to numerical vectorsīy a simple mapping starting with A=0 and so on.
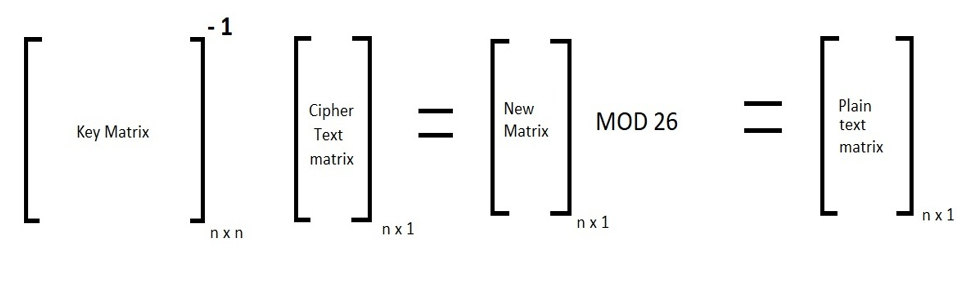
Let the order of the encryption key be N (as it is a square matrix). Modern linear algebra techniques to encode and decode text using an encryption The 'HillCipher' class below implements the Hill Cipher algorithm which uses


 0 kommentar(er)
0 kommentar(er)
